What I'm looking for at CES

If you like to experience sensory overload, go to CES. 3200 exhibitors, hundreds of large-screen TVs hanging off the ceiling, celebrity appearances, flashy cars, and of course Las Vegas outside the convention center.

Here's what I'm looking to see at CES:

• The latest and greatest in portable (man worn) display technologies. Would love to see which are ready for prime time within a Sensics product.
• All kinds of sensors: motion sensors, hand and finger sensors, biometric sensors, eye trackers, full body sensing, proximity sensors, embedded cameras for augmented reality. In short, anything that can be reasonably combined with a VR goggle to create the next-generation experience.
• Companies that have VR/AR ideas and concepts and unique specifications but need help in refining these specifications and then building high-performance and affordable products around them. In the last year, my company has done several such projects and have the designs, IP and decade of experience to help. High-end gaming goggle? Unique display or signal processing requirements? We can help.
• Last, catch up with friends and professional acquaintances. It's not often that so many of my network are in the same city at the same time.

Whether you are 'buying' or 'selling' in these categories, drop me a note and perhaps we can meet at the show.

Happy Holidays to all. Rest well and get ready for CES 2014!

The VR goggle as a Sensory and Computing platform

While there is still a lot of work to do on display technologies and optics to get the best possible image in front of the eyes, the real promise of virtual reality goggles is to serve as a portable sensory and computing platform.

Goggles are becoming a platform for several reasons:

• They are a physical platform. Once you securely position goggles on the head, you now have a physical base to attach additional sensors and peripherals: cameras, trackers, depth sensors and more.
• Portable computing is becoming evermore powerful, thereby creating an incentive to process and analyze sensory data on the goggles as opposed to transmitting large amount of information to some computing base. Furthermore, a key part of the value of goggles is their portability, so the ability to process 'locally' - on the goggle - contributes to the realization of this value.
• As goggles become increasingly immersive, the value of sensors increase as a way to tie the experience into physical objects in the immediate surroundings, as well as connect the actions and context of the user to what is happening 'inside' the display.

One could look at the following diagram - courtesy of Sensics - as a good illustration to what these sensors might be:

One could imaging several types of sensors as feeding into the goggle:

• Orientation and position sensors - whether for the head, limbs or objects such as a gaming sword
• Cameras that might provide visible, IR or depth map information
• Positional sensors such as GPS or indoor location sensors
• Eye tracking sensors to understand gaze direction and potentially provide user interface
• Biometric sensors such as heart rate, perspiration, blood pressure. An eye tracker can also provide pupil size which is another biometric input.
• and more

One would then need to turn this sensor data into useful information. For instance, turn position and orientation of various body parts into understanding of gestures; turn a depth map into detection of nearby obstacles; detect faces and markers from a video image.

As we have discussed before, a virtual reality abstraction layer is going to speed up this process as it will allow those that turn data into information to relieve themselves from the need to worry about the particular formats and features of individual sensors and focus on a category of sensors.

There are several places where this transformation could happen: on the goggle with the help of an embedded processor (as shown in the above diagram); Near the goggle on a device such as a tablet or powerful smartphone; At a stationary device such as a desktop PC or gaming console. Performing this transformation in or near the goggle allows running the application software in or near the goggle, leading to a truly portable solution.

What is the best place to do so? As Nelson Mandela - and others - have said "Where you stand depends on where you sit". If you are a PC vendor that is married to everything happening on the PC, you shudder at the notion of the goggle being an independent computing platform. If you are a goggle vendor, you might find that this architecture opens up additional opportunities that do not exist when you are physically and logically tied to a stationary platform. If you are a vendor making phones or tablets, this might allow you to position the phone as a next-generation portable gaming platform.

So, beyond innovations in displays and optics, I think we will see lots of interesting sensors and sensor fusion applications in 2014.

What do you think? Let me know.

Not just micro displays: adding flat panel products to the mix

After about a decade of making virtual reality goggles and other near-eye devices based on micro displays, my company started demonstrating and shipping goggles that are based on flat-panel displays such as those found in smartphones. Many that have visited the I/ITSEC training show in Orlando had a chance to experience some of our new offering, and we were very happy with the feedback received.

It was not a difficult decision. Given the increasing resolution, diverse supplier base and lower cost of flat panel displays (as opposed to OLED micro displays), it made sense to start applying our innovation and our expertise in goggles to this new display technology.

To date, we have exclusively used OLEDs from eMagin. There are many good folks at eMagin, and they have nice products, but given their well-documented delivery challenges and new designs made possible by flat-panel displays, they won't be our exclusive display supplier anymore.

Where and when is it best to use OLED micro displays?

• Where physical space is limited, such as when building a simulated rifle scope
• When the contrast and response time of OLEDs are a must (that is, until OLED flat panels become widely available for goggle use)
• Where harsh environmental conditions - especially temperature - are required, such as in our ruggedized HMD for training
• Where high pixel density is required
• Where being able to purchase replacement parts for many years is important
• When low power consumption is critical

Where and when is it best to use flat panel displays?

• Where wide field of view is particularly important
• When it is important to have supplier diversity
• When cost is a major factor

Not married to one display technology or another, it is now possible to choose the best one for each new product.

Do you make your own [...]?

Quite often, I get asked whether my company makes specific components - motion trackers, electronics, optics, etc. - that we use inside our virtual reality goggles.

As one would expect, we look at these 'make vs. buy' decisions individually, and ask several questions:

• Can we add value to our customers if we 'make'? Can we generate a product that is significantly better or lower-cost or offers some other unique benefits relative to the 'buy' alternative?
• How many of these do we expect to make? We'd be much more likely to buy when only small quantities are required and more inclined to make when there are more units.
• Can we afford it?
• Can we build it on time?
• Can we create value for our shareholders by generating valuable patent filings or know-how?
• Is this a discipline that we need to understand very well for our future business?
• Does a 'buy' option exist?

Historically, these have been our answers:

• Orientation trackers: we typically buy, but we then try to improve what we buy. We have worked with many of the leading orientation tracking vendors - Intersense, Intertial labs, Hillcrest, YEI - and have decided against developing our own. However, we have often worked with these manufacturers to introduce new features in their products or to optimize them for HMD use. We have added some of our own features such as predictive tracking when those did not exist. Last, we prefer to encapsulate the vendor-specific API with a standard Sensics interface because it allows our customers the benefit of maintaining their software investments when we change the motion tracker vendor inside our products.
• Optics. To date, we have always designed and made optics ourselves. We have made optics for small and large displays, using glass, plastic and fiber, using a variety of manufacturing technologies. We believe that the our portfolio of optical designs is an advantage, and that optics are a critical part of the goggle experience.
• Electronics. We often design our own electronics. Sometimes, we need special high-speed processing, and in other instances, we feel that we need something beyond simple driving of a display. This can be unique video processing, distortion correction or packaging that supports a particularly compact design.
• Displays. We buy. We don't have the know-how nor the capital to make our own displays and in the world of changing display technologies, we're glad not to be locked into a specific one. Having said that, we have worked with eMagin in prior years to modify the size of one of their OLED driver boards to make a system more compact and achieve better optical design. It was a financial investment, but we felt we added value to our customers.
• Mechanical design. We rarely design accessories such as helmet-mounts, but we do love to design goggle enclosures whether to give it our unique 'look', or to include innovative features such as hand tracking sensors.
• Software. We write our own (or pay to have it written). Our software is so deeply tied to the unique functionality of our designs that it is not available for off-the-shelf purchase.

If you are a manufacturer and would like to see how we can use some of our technologies to help you get new, innovative products to market on short order, drop me a line.

An Interview with Sebastien Kuntz, CEO of "I'm in VR"

Following my blog post "Where are the VR abstraction layers" I had an opportunity to speak with Sebastien Kuntz, CEO of "I'm in VR" a Paris-based company that is attempting to create such layers. I've known Sebastien for several years, since he was part of Virtools (now Dassaut Systemes) and it was good to catch up and get his up-to-date perspective.

Sebastien Kuntz, CEO of "I'm in VR"

Sebastien, thank you for speaking with me. For those that do not know you, please tell us who you are and what you do?

My name is Sebastien Kuntz and I am CEO of "i’m in VR". Our goal is to accelerate the democratization of virtual reality and towards that goal we created the MiddleVR middleware software product. I have about 12 years of experience virtual reality, starting at the French Railroad company working on immersive training, and continuing as the lead VR engineer in Virtools, which made 3D software. After Virtools was acquired by Dassault Systemes, I decided to start my own company and that is how "i’m in VR" was born.

What is the problem that you are trying to solve?

Creating VR applications is complex because you have to take care of a lot of things – tracking devices, stereoscopy, multiple computers synchronization (if you are working with a Cave), interactions with the virtual environment (VE).

This is even more complex when you want to deploy the same application on multiple VR systems - different HMDs, VR-Walls, Caves ... We want developers to focus on making great applications instead of working on low-level issues that are already solved.
MiddleVR helps you in two ways:

• It simplifies the creation of your VR applications with our integration in Unity. It manages the devices and cameras for you, and offers high-level interactions such as navigations, selection and manipulation of objects. Soon we will add easy-to-use immersive menus, more interactions and haptics feedback.
• It simplifies the deployement of your VR applications on multiple VR systems: the MiddleVR configuration tool helps you easily create a description of any VR system, from low-cost to high-end. You can then run your application and it will be dynamically reconfigured to work with your VR system without modification.

MiddleVR is an easy-to-use, modern and commercial equivalent of Cavelib and VR-Juggler.

How do you provide this portability of a VR application to different systems ?

MiddleVR provides several layers of abstraction.

• Device drivers: the developers don't have a direct access to native drivers, they have access to what we call "virtual devices", or proxy devices. The native drivers write tracker data like position and orientation directly in such a "virtual device". This means that we can change the native drivers at runtime while the application is still referencing the same "virtual device".  
• Display: all the cameras and viewports are created at runtime depending on the current configuration. This means your application is not dependent on a particular VR display.
• 3D nodes: Most of the time the developer does not care about the information from a tracker, he is more interested in the position of the user's head or hand for example. MiddleVR provides a configurable representation of the user, whose parts can be manipulated by tracking devices. For example the Oculus Rift orientation tracker can rotate the 3D node representing the user's head, while a Razer Hydra can move the user's hands. Then in your application you can simply ask "Where is the user's head ? Is his hand close to this object ?", which does not rely on any particular device. This also has the big advantage of putting the user back in the center of the application development!
• Interactions: At an even higher level, the choice of an interaction technique is highly dependent on the characteristics of the hardware. If you have a treadmill you will not navigate in a VE in the same way as if you only have a mouse, or a joystick, or if you want to use gestures... The choice of a navigation technique should be made at runtime based on the available hardware. In the same way, selecting and manipulating an object in a VE can be made very efficient if you use the right interaction techniques for your particular hardware. This is work in progress, but we would like to provide this kind of interactions abstraction. We are also working on offering immersive menus and GUIs based on HTML5.

Will this interaction layer also allow you to define gestures?

Yes, the interaction layer will certainly allow you to define and analyze gestures. Though this particular functionality is not yet implemented in the product, you will be able to integrate your own gestural interactions.

Do you extend Unity's capabilities specifically for VR systems ?

Yes we provide active stereoscopy, which Unity cannot do.
We also provide application synchronization on multiple computers, which is required for VR systems such as Caves. We synchronize the state of all input devices, Unity physics nodes, the display of new images (swap-buffer locking) and left/right eye images display in active stereo(genlocking). As mentioned, we will also offer our own way of creating immersive menus and GUIs because Unity’s GUI system has a hard time dealing with stereoscopy and multiple viewports. 

Do you support other engines other than Unity?

MiddleVR has been created to be generic, so technically it was designed to be integrated into multiple 3D engines, but have not done so yet. It’s the usual balance of time and resources. We made several promising prototypes though.

How far are we from true ‘plug and play’ with regards to displays, trackers and other peripherals?

We are not there yet. You need a lot more information to completely describe a VR system than most people think.

First, there is no standard way to detect exactly which goggle, tv, projector or tracker is plugged in. [Editor's note: EDID does provide some of that information]

Then in a display (HMD, 3D monitor, CAVE), it is not enough to describe resolution and field of view. You also need to understand the field of regard. With an HMD you can look in all directions. With a 3D monitor or most CAVEs, you are not going to be able to see an image if you look towards the back. The VR middleware needs to be aware of this and allow interaction methods that adapt to the field of regard. Moreover you have to know the physical size of the screens to compute the correct perspective. 

I believe we should describe a VR system not based on its technical characteristics such as display resolution or number of cameras for optical tracking, but rather in terms of what those characteristics means for the user in terms of immersion and interaction! For example:

• What is the end-to-end latency of the VR system for each application? This will directly influence the overall perception of the VE.
• What is the tracking volume and resolution in terms of position and orientation? This will directly influence how the user interacts with the VE: we will not interact the same with a Leap Motion which has a small tracking volume, or with the Oculus Rift tracker which can only report orientations or with 20 Vicon cameras able to track a whole room with both positions and orientations.
• What is the angular resolution of the display? If you can't read a text from a given distance, you will have to be able to get the text closer to you. If you can read the text because your VR system has a better angular resolution, you don't necessarily need this particular interaction.
• What is the field of regard ? As discussed above this also influences your possible actions.

The user's experience is based on its perceptions and actions, so we should only be talking about what is influencing those parameters. This requires a bit more work because they are highly dependent on the final integration of the VR system.

We are not aware of standards work done to create these ‘descriptors’ but we would certainly support such effort as it would benefit the industry and our customers.

Are most of your customers today what we would call ‘professional applications’ or are you seeing game companies interested in this as well?

Gaming in VR is certainly gaining momentum and we are very interested in working with game developers on creating this multi-device capability. We are already working with some early adopters.

We are working hard to follow this path. For instance, we are about to release a free edition of MiddleVR based on low-end VR devices and would like to provide a new commercial licence for this kind of developments. This is in our DNA, this is why we were born! We want to help the current VR democratisation. 

When you think about porting a game to VR, there are two steps (as you have mentioned in your blog): the first one is to adapt the application to 3D, to motion tracking ,etc. This is something you need to do regardless of the device you want to use.

The second is to adapt it to a particular device or set of devices. We can help with both, and especially with the 2nd step. There will be many more goggles coming to market in the next few months. Why just write for one particular VR system when you can write a game that will support all of them ?

What’s a good way to learn more about what MiddleVR can do for application developers? Any white paper or video that you recommend?

Our website has a lot of information. You can find a 5 minutes tutorial, and here another video demonstrating the capabilities of the Free edition.

Sebastien, thank you very much for speaking with me. I look forward to seeing more of I'm in VR in action.

Thank you, Yuval

Can the GPU compensate for all Optical Aberrations?

Photo Credit: davidyuweb via Compfight cc

As faster, newer Graphics Processing Units (GPUs) become available, graphics cards can perform real-time image transformations that were previously relegated to custom-designed hardware. Can these GPUs overcome all the important optical aberrations, thus allowing HMD vendors to use simple, low-cost optics?

The short answer is: GPUs can overcome some, but not all aberrations. Let's look deeper into this question.

Optical aberrations are the result of imperfect optical systems. Every optical system is imperfect, though of course some imperfections are more noticeable than others. There are several key types of aberrations in HMD optics which take an image from a screen and pass it through viewing optics:

• Geometrical distortion, which we covered in a previous post would cause a square image to appear curved. The most common variants are pincushion distortion and barrel distortion.
• Color aberration. Optical systems impact different colors in different ways, as can be seen in a rainbow or when light passes through a prism. This results in color breakup where a white dot in the original screen breaks up into its primary colors when passing through the optical system.
• Spot size (also referred to as astigmatism), which shows how a tiny dot on the original screen appears through the optical system. Beyond the theoretical limits (diffraction limit), imperfect optical systems cause this tiny dot to appear as a blurred circle or ellipse. In essence, the optical system is unable to perfectly focus each point from the source screen. When the spot size becomes large enough, it blurs the distinction between adjacent pixels and can make viewing the image increasingly difficult.

The diagram below shows an example of the spot size and color separation on various points in the field of view of a certain HMD optical system. This is shown for the three primary colors, with their wavelengths specified in the upper right corner. As you can see, the spot size is much larger for some areas than others, and colors start to appear separated.

Which of these issues can be corrected by a GPU, assuming no practical limits on processing power?

Geometrical distortion can be corrected in most cases. One approach is for the GPU to remap the image generated by the software so that it compensates for known optical distortion. For instance, if the image through the optical system appears as if the corners of a square are pulled inwards, the GPU would morph that part of the image by pushing these corners outwards. Another approach is to render the image up-front with the understanding of the distortion, such as the algorithm covered in this article about an Intel researcher.

Color aberration may also be addressed, though it is more complex. Theoretically, the GPU can understand not only the generic distortion function for a given optical system, but the color-specific one as well, and remap the color components in the pixels accordingly. This requires understanding not only the optical system but also the primary colors that are being used in a particular display. Not all "greens", for instance, are identical

Where the GPU fails is in correcting astigmatism. If the optical system causes some parts of the image to be defocused, the GPU cannot generate an image that will 're-focus' the system. In simpler optics, this phenomena is particularly noticeable away from the center of the image. 

One might say that some defocus in the edge of an image is not an issue since the central vision of a person is much better then the peripheral vision, but this argument does not take into account the rotation of the eye and the desire to see details away from the center.

Another discussion is the cost-effectiveness of improving optics, or the "how good is good-enough" debate. Better optics often cost more, perhaps weigh more, and not everyone needs this improved performance or is willing to pay for it. Obviously, less distortion is better to more distortion, but at what price?

Higher-performance GPUs might cost more, or might require more power. This might prove to be important in portable systems such as smartphones or goggles with on-board processors (such as the SmartGoggles), so fixing imperfections on the GPU is not as 'free' as it might appear at first glance.

HMD design is a study in tradeoffs. Modern GPUs are able to help overcome some imperfections in low-cost optical systems, but they are not the solution to all the important issues.

For additional VR tutorials on this blog, click here
Expert interviews and tutorials can also be found on the Sensics Insight page here

Where are the VR Abstraction Layers?

"A printer waiting for a driver"

Once upon a time, application software included printer driver. If you wanted to use Wordperfect, or Lotus 1-2-3, you had to have a driver for your printer included in that program. Then, operating systems such as Windows or Mac OS came along and included printer drivers that could be used by any application. Amongst many other things, these operating systems provided abstraction layers - as an application developer, you no longer had to know exactly what printer you are printing to because the OS had a generic descriptor that told you about the printer capabilities and provided a standard interface to print.

The same is true for game controllers. The USB HID (Human Interface Device) descriptor tells you how many controls are in a game controller, and what it can do, so when you write a game, you don't have to worry about specific types of controllers. Similarly, if you make game controllers and conform to the HID specifications, existing applications are ready for you because of this abstraction layer.

Where are the abstraction layers for virtual reality? There are many types of VR goggles, but surely they can be characterized by a reasonably simple descriptor that might contain:

• Horizontal and vertical field of view
• Number of video inputs: one or two
• Supported video modes (e.g. side by side, two inputs, etc.)
• Recommended resolution
• Audio and microphone capabilities
• Optical distortion function
• See through or immresive configuration
• etc

Similarly, motion trackers can be described using:

• Refresh rate (e.g. 200 Hz)
• Capabilities: yaw, pitch, roll, linear acceleration
• Ability to detect magnetic north
• etc,

Today, when an application developer wants to make their application compatible with a head-mounted display, they have to understand the specific parameters of these devices. The process of enhancing the application involves two parts:

1. Generic: change the application so that it supports head tracking; add two view frustums to support 3D; modify the camera point; understand the role of the eye separation; move the GUI elements to a position that can be easily seen on the screen; etc.
2. HMD-specific: understand the specific intricacies of an HMD and make the application compatible with it

If these abstraction layers widely existed, the 2nd step would be replaced by supporting the generic HMD driver or head tracker driver. Once done, the manufacturers would need to write a good driver and viola! users can start using their gear immediately.

VR application frameworks like Vizard from WorldViz provide an abstraction layer, but they are not as powerful as modern game engines. There are some early efforts such as I'm in VR to provide middleware, but I think a standard for an abstraction layer has yet to be created and gain serious steam. What's holding the industry back?

UPDATE: Eric Hodgson of the Redirected Walking fame reminded me of VRPN as an abstraction layer for motion trackers, designed to provide a motion tracking API to applications either locally or over a network. As Eric notes, VRPN does not apply to display devices but does abstract the tracking information. I think that because of it being available on numerous operating systems, VRPN does not provide particularly good plug-and-play capabilities. Also, it's socket-based connectivity is excellent for tracking devices that, at most, provide several hundred lightweight messages a second. To be extended into HMDs, several things would need to happen, including:

• Create a descriptor message for HMD capabilities
• Plug and play (which would also be great for the motion tracking)
• The information about HMDs can be transferred over a socket, but if the abstraction layer does anything that is graphics related (in the same way OpenGL or DirectX abstract the graphics card), it would need to move away from running over sockets.

Is Wider Field of View always Better?

I have always been a proponent of wide field of view products. The xSight and piSight products were revolutionary when they were introduced, offering a combination of wide field of view and high resolution. There is widespread agreement that wide field of view goggles provide greater immersion, and allow users to perform many tasks faster and better.

Johnson's Criteria for
detection, recognition and identification -
from Axis Communications

But for a given display resolution, is wider field of view always better? The answer is 'No' and thinking about this question provides an opportunity to understand the different set if requirements between professional-market applications of virtual reality goggles (e.g. military training) and gaming goggles.

Aside from the obvious physical attributes - pro goggles often have to be rugged - the professional market cares very much about pixel density (or the equivalent pixel pitch) because it determines the size and distance of simulated objects that can be detected. For instance, if you are being trained to land a UAV, or trying to detect a vehicle in the distance, you want to detect, recognize and identify the target as early as possible and thus as far away as possible. The farther the target appears away, the fewer pixels it occupies on the screen for a given pixel density.

The question of how exactly many pixels are required was answered more than 50 years ago by John B. Johnson in what became known as the Johnson Criteria. Johnson looked at three key goals:

• Detection - identifying that an object is present.
• Recognition - recognizing the type of object, e.g. car vs. tank or person vs. horse.
• Identification - such as determining the type of car or whether a person is a male or a female.

Based on extensive perceptual research, Johnson determined that to have a 50% probability that an observer would discriminate an object to the desired level, that object needs to occupy 2 horizontal pixels for detection, 8 horizontal pixels for recognition and 13 horizontal pixels for identification.

Let's walk through a numerical example to see how this works. The average man in the United States is 1.78m tall (5' 10") and has a shoulder width of about 46cm (18"). Let's assume that a simulator shows this person at a distance of 1000 meters. We want to be able to detect this person inside an HMD that has 1920 pixels across.

46 cm makes an angle of 0.026 degrees (calculated using arctan 0.46/1000). At a minimum, we need this angle to be equivalent to two pixels. Thus, the entire horizontal field of view of this high-resolution HMD can be no more than 25.3 degrees for us to achieve detection. If the horizontal field of view is more than that, target detection will not be possible at these simulated distances.

Similarly, if we wanted to be able to identify that person at 100 meters, these 46 cm would make an angle of 0.26 degrees so the horizontal field of view of our high-resolution 1920 pixel HMD can be no more than 38.9 degrees. If the horizontal field of view is more than that, target identification will not be possible at these simulated distances.

Thus, while we all love wide field of view, thought must be put into the field of view and resolution selection depending on the desired use of the goggles.

Notes:

• Johnson's article was "John Johnson, “Analysis of image forming systems,” in Image Intensifier Symposium, AD 220160 (Warfare Electrical Engineering Department, U.S. Army Research and Development Laboratories, Ft. Belvoir, Va., 1958), pp. 244–273."
• Johnson's work was expressed in line pairs, but most people equate a line pair to a pair of pixels.
• Johnson also looked at other goals such as determining orientation, but detection, recognition and identification are the most commonly-used today.

Thoughts on the Future of the Microdisplay Business

If I were a shareholder of a microdisplay company such as eMagin or Kopin, I'd be a little worried about where future growth is going to come from.

For years, the microdisplay pitch was something like this: we make microdisplays for specialized applications - such as military products - where high performance are required, sometimes coupled with the ability to withstand harsh environments. One day, there will be a consumer market for such products in the form of virtual reality goggles or high-quantity of camera viewfinders, and this will allow us to reduce the price of our products and expand our reach. While this is coming, we make money by selling our specialized markets and doing contract research work.

This pitch is starting to look problematic. The consumer market is waking up, but not necessarily to the displays made by eMagin and Kopin.

In immersive virtual reality (e.g. not a see-through system), smartphone displays are a much more economical solution. Because more than a hundred million smartphones are sold every year, the cost of a high-resolution smartphone display can easily be less than 5% the cost of a comparable microdisplay. Microdisplay pricing has always been a chicken-and-an-egg game: prices can go down if quantities increase, but quantities will increase only if prices go down AND enough capital is available for production line and tooling investments.

Other technologies are also good candidates: pico projectors might become very popular for heads-up displays in cars and once large quantities will be made, they can also replace the microdisplay as a technology of choice.

Pico projectors are physically small which might be attractive to see-through goggles similar to Google Glass. The current generation of see-through consumer products does not seek to be high resolution nor wide field of view, and thus low-cost LCOS displays (Google is reportedly using Hynix) can provide a good solution for a high-brightness display that can be used outdoors. Karl Guttag had an interesting article on why Kopin's transmissive displays are not a good fit for these kind of applications.

One more thing on the subject of microdisplay prices. Though the financial reports do not reveal that microdisplays are a terrifically-profitable business, I suspect prices are also kept at some level because of "most favored nation" clauses to key customers such as perhaps the US government. Such clauses might force a microdisplay company that reduces prices to offer these reduced price levels to these 'most favored' customers. Thus if - for example - the US government is responsible for a large portion of a company's revenue and has a most-favored nation clause, any reduction in pricing beyond what is offered to the government will immediately results in significant loss of revenue once the US government prices are also reduced.

There will always be specialized applications where a display like eMagin's can be a perfect fit. Perhaps ones that requires very small physical size (such as when installed in a simulated weapon), or ones that can withstand extreme temperature and shock, or ones where quality is paramount and cost is secondary, but these do not sound like high-volume consumer applications.

The financial reports of both eMagin and Kopin reflect this reality. Both companies are currently losing money as they seek to address this reality.

What can be done to expand the business? One option is vertical integration. An opto-electronic system using a display needs additional components such as driver boards and optics beyond the display.  Today, these come from third-party vendors but one could imagine micro-display companies offering electronics and optics - or maybe even motion trackers - for small to medium-sized production runs. Another option which is currently pursued by Kopin is offering complete platforms and systems such as the Golden-i platform. Ostensibly, the margins on systems are much higher than the margin on individual components, especially as these become commodities. Over time, perhaps there is greater intellectual property there as well.

It will be interesting to see how this market shakes out in the upcoming months.

Full disclosure: I am not a shareholder of either company but my company uses eMagin microdisplays for several of our products.

Comprehensive hand and finger tracking? Try sensor fusion

A wide variety of applications could benefit from hand and finger tracking, but the performance requirements are quite diverse.

• For some applications, understanding the position of the hand as a point in space would be sufficient. Virtual boxing, for instance.
• For some, 360 degree tracking of the hands would be useful. A throwing motion of a football quarterback starts from behind the head. 
• Those applications needing finger tracking can often do with the fingers in front of the body, though if the finger sensor is mounted on the head, its field of vision might not be enough of the head is turned one way - say left - while the tracked hand goes right.

I think the solution will be some hybrid of the various technologies. Whether it is something like the Sixense STEM, YEI PrioVR, structured light technologies (like the one implemented in the Kinect), Time of Flight (inside the new Kinect), these technologies would need to be combined for a truly effective solution.

Progress in Hand and Body Tracking

I continue to believe that putting a display on the head, as great as that display might be, is not enough for a truly compelling virtual reality interaction, and that hand and finger tracking is a critical missing component for the VR experience.

Two new Kickstarter projects provide a step in the right direction, each taking a different approach:

Approach 1: PrioVR from YEI

PrioVR from YEI Technology has launched on Kickstarter earlier this month. It uses a connected network of high-quality orientation sensors to determine the orientation of various body parts. By logically connecting these sensors to a skeletal model of the body, the system can also determine the body posture and position of hands, feet, elbows, etc. This facilitates both motion capture as well as real-time reporting of body position and orientation into a game engine.

Motion Capture studio from YEI technology

One of the things that I like about the PrioVR system is that it is completely portable. It does not require a stationary sensor (e.g. Kinect), it does not require the person to be facing towards a particular direction and can really be taken anywhere, assuming you are willing to walk around with the sensors strapped to the body. The system does assume a wireless link between the central station on the body and a computer, but this works over fairly substantial distances. Additionally, if the computing device is portable, one could imagine a simple wired connection to it for enhanced portability.

The fidelity of the model is dependent on many parameters, including:

• The number of sensors that are being used. For instance, if a sensor is placed on the back, this sensor can be used to determine the rotation of the body and also help in determining the XYZ position of head (leaning forward will be registered in the system and through the skeletal model can be used to estimate the height of the head). However, if another sensor is placed on the lower back, the combination of these two sensors can be used to determine if the person has turned or is twisting the back.
• Calibration accuracy. In the YEI model, sensors are attached to the body using elastic straps. It is easy to see how a strap might be rotated so that, for instance, an arm sensor is not parallel to the ground even when the arms are. To avoid errors, a quick calibration might be required at the beginning of a session. 
• Accuracy of skeletal model. If the model assumes a certain distance from shoulder to elbow, but the actual distance is different that what is assumed, one could see how the hand position might be impacted by this skeletal error.

One wonders if this system does not produce 'too much information' relative to what is required. For instance, while it may be nice to understand if the arm is bent and exactly at what direction, is that information really required for a game that only cares about the hand position?

Approach 2: STEM from Sixense

The STEM system is scheduled to launch on Kickstarter later this month. It is an enhanced version of the current Razer Hydra in the sense that it adds wireless controllers as well as additional tracking points.

The STEM system uses a base station that helps track the XYZ position of various sensors/endpoints. A typical use case would be to track both hands when the user is holding a wireless controller as well as to track additional devices (head, weapon, lower body) if sensing modules are placed on it. To some extent, this is a simpler and more direct method than the PrioVR solution. With STEM, if you want to know the position of the hand, you just put a sensor on the hand. With PrioVR, if you want to know the position of the hand, you have to deduce it from the orientation of the various bones that make up the arm as well as knowledge about the upper and lower body. At the same time, it provides fewer data points about the exact posture and perhaps is more limited in the number of simultaneous sensors.

I have not had a chance yet to thoroughly evaluate the accuracy and response time of the STEM system yet.

Sixense STEM controller

Once the basic position and orientation data is presented to the application from either the PrioVR or STEM sensors, there is still an opportunity for a higher level of processing and analysis. For instance, additional software layers can determine gestures or hand signals. If more processing can be done in a middleware software layer, less processing will be required by the games and other applications to take advantage of these new sensors.

Another open question for me is the applicability to multi-person scenarios, assuming more than one 'instrumented' person in the same space. How many of these devices can be used in the same room without cross-interference.

Having said all that, I am excited by both these products. They are very welcome steps in the right direction towards enhancing and potentially revolutionizing the user experience in virtual reality.

Overcoming Optical Distortion

In a previous post, we discussed what optical distortion is and why it is important. In this post, we will discuss ways to correct or overcome distortion.

jenny downing via Compfight cc

There are four main options:

1. Do nothing and let users live with the distortion. In our experience, geometrical distortion of less than 5-7% is acceptable for mainstream professional applications. One of our competitors in the professional market made a nice living for several years by selling an HMD that had close to 15% distortion. However, some customers felt that it was good enough and that the HMD had other things going for it, such as low contrast and high power consumption. For gaming, it may be that larger distortion is also acceptable.

2. Improve the optical design. Lower distortion can certainly be a design goal. However, the TANSTAAFL principle holds ("There ain't no such thing as a free lunch", as popularized by Robert Heinlein) and to get lower distortion, you'd typically have to agree to relax other requirements such as weight, material selection, eye relief, number of elements, cost, transmissivity or others. Even for a standard eMagin SXGA display, my company has found that different customers seek different sets of requirements, which is why we offer two different OEM modules for this display, one design with lower weight and the other with lower distortion and generally higher performance.

3. Fix it in the GPU. The Graphics Processing Unit (GPU) of a modern graphics card or the GPU embedded inside many ARM chips are capable of performing geometry remapping to accommodate the geometrical distortion in the optics in a process called texture mapping. The upside of this approach is that it does not increase the direct system cost. The downside is that it requires modifying the program generating the content. If the content comes from a source that you have less control of (such as a camera, or a game that you previously purchased), you are unable to correct for the distortion.

4. Correct it in the goggle electronics. One could construct high-speed electronics (such as these) that perform real-time distortion correction for a known distortion function. This adds cost and complexity to the system but can work with any content regardless of where it came from. Done correctly, it need not add significant latency to the video signal.

Additional options, often application-dependent, also exist. For instance, we have several customers that use the goggles to present visual stimuli to their subjects. If the stimuli are simple such as a moving dot on the screen, the program generating them can take into account the distortion function while generating the stimuli, thus correcting for the distortion without help from the GPU



For additional VR tutorials on this blog, click here
Expert interviews and tutorials can also be found on the Sensics Insight page here.

"Packed like a Jar"

I'm back from a Tuscany vacation (the real Tuscany, not the Sixense VR demo) and back to blogging.

Photo Credit: origamidon via Compfight cc

Today, I want to talk about packaging for virtual reality equipment and how it relates to customer experience.

A few years ago, my company was primarily selling the xSight HMD, which is a fairly unique product in its field of view (>120 degrees), resolution (HD1080 per eye) and weight (350 grams). However, the xSight uses tiled displays - several small displays that are optically combined into a larger image. Some people love it. Others, not so much. Bottom line - we were closer to 'built to order' than to 'mass production'.

Our packaging used to be a standard brown cardboard box, and the founder of the company would labor to fill it up with rolled bubble wrap for maximum protection. Indeed, these packages almost always survived the "viking with a spear treatment" afforded to them by our shipping partners.

One day, we got an email from one of our resellers saying that they received the product and that 'it is packed like a jar from eBay'. I don't think she meant it as a compliment, though one could imagine that jars are usually packed in such a way that they will arrive unharmed at the destination.

That got us thinking about customer experience and branding.

As our products grew more popular, we invested some in custom reusable packaging, so that everything had a place in the box, and that the box could be used again and again for shipping units from one place to another.

Then, we realized we had all these Sensics boxes going shipping around with no clear branding on them. We purchased custom packing tape with the logo and eventually settled on a custom box with the logo already printed on it.

Having protected the unit, no longer looking like a jar, we went to think about the customer experience: what do we want our customer to first see when they open the box. Is it a big reminder to register their product? Is it a cable? We figured the best thing is a large 'THANK YOU' note that also talks about how to best reach us in case there is any question or problem.

Then, we started looking at the user manual. Is it too long? Do we need a quick-start guide? Better yet, can you just 'plug it in and go'? Are we providing all the cables that you might reasonably need to use our product? Are the cables consistent and are of high quality? Is the software DVD easy to use? Does it professionally show the product name on it for easy identification?

If a product needs repair, is it easy to contact us? We are now tracking time to first respond to customer service requests. We now offer 3 year warranty on many products. 

Do we have room to improve? Absolutely! But the reseller that asked us about the jar got us thinking in the right direction, and we (as well as our customers, I think) thank her for that.

What is Geometric Distortion (and Why Should you Care)?

What is Geometric Distortion?

Geometric distortion is a common and important type of optical distortion that occurs in VR goggles as well as in other optical systems. In this post we will discuss the types of geometric distortion and ways to measure the distortion. There are additional types of optical distortions, such as chromatic aberration, and we will discuss some of them in future posts.

Geometric distortion results in straight lines not being seen as straight lines when viewed through the goggle optics.

What are common types of geometric distortion?

The two common types of distortion are barrel distortion and pincushion distortion. These are shown in the figure below. The left grid is the original image and next to it are pincusion distortion and barrel distortion.

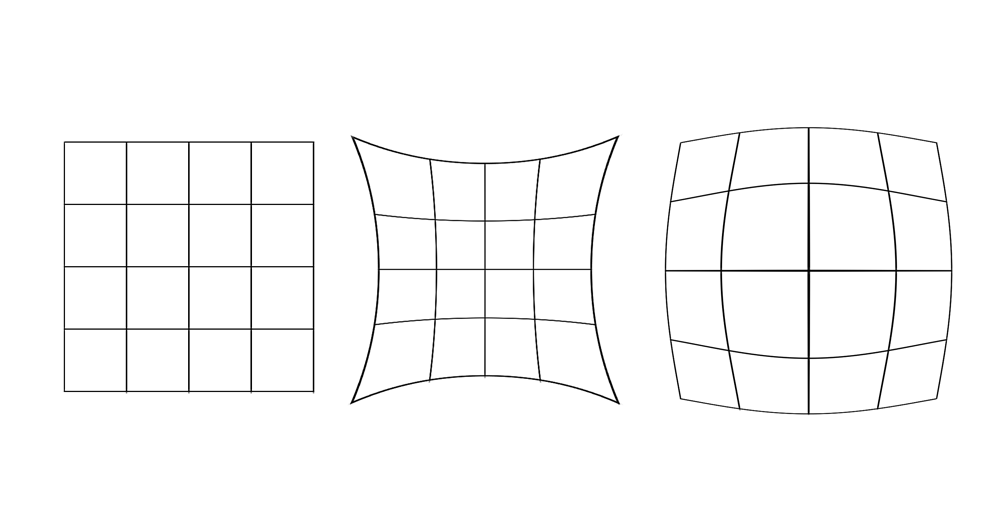Sourcr: Wikipedia

A barrel distortion is one where the perceived location of a point in space (e.g. the intersection of two of the grid lines) is farther away from the center relative to where it really is. A pincushion distortion is one where the perceived location of a point in space is closer from the center relative to where it really is. Both these distortions are often radial, meaning that the amount of distortion is a function of how far a point is relative to the optical axis (e.g. the center of the lens system). The reasons distortions are radial is that many optical systems have radial symmetry.

Geometric distortion and VR Goggles

Geometric distortion is inherent to lens design. Every lens or eyepiece have some geometric distortion, though it is sometimes not large enough to be noticeable. When designing an eyepiece for a VR goggle, some maximum allowable geometric distortion is often a design goal. Because VR eyepieces need to balance many other desires - minimal weight, image clarity, large eye relief (to allow using goggles while wearing glasses), large eye box (to accommodate left/right/up/down movements relative to the optimal eye position) - the distortion is just one of many parameters that need to be simultaneously optimized.

Photo of a test grid through goggle optics. Picture taken using iPhone camera

Why should you care? Geometric distortion is important for several reasons:

• If left uncorrected, it changes the perceptions of objects in the virtual image. Straight lines appeared curved. Lengths and areas are distorted. 
• In a binocular (two-eyed) system, there is an area of visual overlap between the two eyes, which is called binocular overlap. If an object is displayed in both eyes in this area, and if the distortion in one eye is different than the other (for instance, because the object's distance from center is different), a blurry image will often appear
• Objects of constant size may appear to change size as they move through the visual field.

How is distortion measured?

Distortion is reported in percentage units. If a pixel is placed at a distance of 100 pixels (or mm or degrees or inches or whichever unit you prefer) and appears as if it at a distance of 110, the distortion at that particular point is (110-100)/100 = 10%.

During the process of optical design, distortion graphs are commonly viewed during the iterations of the design. For instance, consider the distortion graph below:

Distortion graph. Source: SPIE

In a perfect lens, the "x" marks should reside right on the intersection of the grid lines. In this particular lens, that is quite far from being the case.

Distortion can also be measured by showing a known target on the screen, capturing how this target appears through the optics and then using specialized software programs to determine the distortion graph. One instance where this is done is during the calibration of a multi-projector wall.

Many distortion functions can be represented as odd-degree polynomials, where 5th or 7th degree is typically sufficiently precise. In formulaic terms:

Typical geometric distortion function

where "r" is the original distance from the center of the image, "a","b","c","d" and "e" are constants and "R" is the apparent distance after the distortion introduced by the optical system. "a" is usually 0.

With any of the above techniques, the constant coefficients can be determined using curve-fitting calculations.

The above also serves a the key to fixing distortion. If it is desired to have a pixel appear to the user in a known distance "R" from the center of the screen, one could solve for "r" above and determine where to put that pixel. For instance, if a system has constant 10% radial distortion as in the example above, placing a pixel at distance 100 would appear as if it is at distance 110. However, placing a pixel at a distance of approximately 91 pixels from center would appear as if it is at distance 100.

The fact that most distortion functions are radial and polynomial also allows for empirical determination. For instance, Sensics has a software program which allows the user to change the coefficients of the polynomials while looking at simulated grid through an optical system. When the coefficients change, the grid changes and this can be done interactively until an approximate correction function for the distortion is discovered

What's next?

In the next post, we will cover several ways to fix or overcome geometric distortions.



For additional VR tutorials on this blog, click here
Expert interviews and tutorials can also be found on the Sensics Insight page here

Interview on Redirected Walking with Professor Eric Hodgson

Prof. Eric Hodgson

My previous post regarding redirected walking generated a good bit of interest, so I decided to dive deeper into the subject by interviewing Prof. Eric Hodgson of Miami University in Ohio, a true expert on the subject.

Eric, thank you for speaking with me. For those that do not know you, please tell us who are you and what do you do?

I'm a psychologist and professor at Miami University (the original one in Ohio, not that *other* Miami). I split my time between the Psychology department -- where I use virtual environments to study spatial perception, memory, and navigation -- and the interdisciplinary Interactive Media Studies program, where I teach courses in 3D modeling, data visualization, and virtual reality development to students from all across the university. I help oversee two sister facilities at Miami, the HIVE (Huge Immersive Virtual Environment) and the SIVC (Smale Interactive Visualization Center). The HIVE is a HMD-based facility with an 1,100 square meter tracking area. The SIVC houses a 4-walled CAVE along with several other 3D projection systems, immersive desktops, development labs, and several motion-capture systems. The HIVE has been funded mostly by the National Science Foundation, the Army Research Office, and the Ohio Board of Regents. The Smale Center was started with a $1.75m gift from the late John Smale, a former CEO of Proctor & Gamble, which uses CAVEs and other visualization systems in their R&D cycle.

You are the director of Smale Interactive Visualization Center. What kind of work is being performed at the Center?

It's a multi-disciplinary center, and a large part of my job is to enable students and faculty from across to university to leverage VR for their work, especially if they don't have the skillset to do it themselves. We also work with regional, national, and international industry partners on specific projects. The work can vary widely, which I find interesting and encouraging -- VR is becoming a very general-purpose tool rather than a niche for a few narrow fields. One of our first projects was building an immersive, 3D Mandala for the Dali Lama for his visit to campus. We've also done motion capture of proper violin-playing arm motion for the music department, developed medical training simulations for the nursing program, developed experiments to study postural sway with psychology, done interactive virtual walk-thoughs of student-designed architectural projects, supported immersive game development, and done work on developing next-generation motion sensing devices and navigation interfaces. Not to mention a 3D visualization of 18th century poetry, which was a collaboration between the Center, the English department, Computer Science, and Graphic Design. I love my job. I also do a lot of tours, field trips, and workshops. When you have a CAVE, a zSpace, a pile of HMDs, and lots of other fun toys (um... I mean tools), you end up being a must-see stop on the campus tour.

A good portion of your research seems to be in the area of redirected walking. Can you explain, in a lay person’s terms, what is redirected walking?

In layman's terms, Redirected Walking is a way of getting people into walking in circles without them realizing it, while it looks like they are walking in a straight line visually. Virtual environments and game levels can be very big; tracking spaces in a lab are typically pretty small. Redirected walking lets immersed users double-back into the same physical space while traveling through a much larger virtual space. There are other techniques that can come into play, such as magnifying or compressing turns, or stretching distances somewhat, but the basic techniques are all aimed at getting people to double back into open physical space so they can keep walking in the virtual environment. It's a bit like the original holodeck on Star Trek... users go into a small room, it turns into an alternate reality, and suddenly they can walk for miles without hitting the walls.

What made you become interested in this area?

Necessity, mostly. I'm a psychologist, studying human spatial cognition and navigation. My colleagues and I use a lot of virtual environments and motion tracking to do our research. VEs allow us to have complete control over the spaces people are navigating, and we can do cool things like moving landmarks, de-coupling visual and physical sensory information, and creating geometrically impossible spaces for people to navigate through. Our old lab was a 10m X 10m room, with a slightly smaller tracking area. As a result, we were stuck studying, essentially, room-sized navigation. There are a lot of interesting questions we could address, though, if we could let people navigate through larger spaces. So, we outfitted a gymnasium (and later a bigger gymnasium) with motion tracking that we called the HIVE, for Huge Immersive Virtual Environment. We built a completely wearable rendering system with battery-powered HMDs, and viola... we could study, um, big-room sized navigation. Since that still wasn't enough, we started exploring Redirected Walking as a way to study truly large-scale navigation in VEs with natural walking.

It seems that one of the keys to successful redirection is providing visual cues that are imperceptible. Can you give us an example of the type of cues and their magnitude?

Some of the recent work we've done uses a virtual grocery store, so I'll use that as an example. Let's say you're immersed, and trying to walk down an isle and get to the milk cooler. I can rotate the entire store around an axis that's centered on your head, slowly, so that you'll end up veering in the direction I rotate the store (really we manipulate the virtual camera, but the end result is the same as rotating the store). The magnitude of the rotation scales up with movement speed in our algorithm, so if you walk faster -- and thus create more optic flow -- I can inject a little bit more course correction. The rotations tend to be on the order of 8 - 10 degrees per second. By comparison, when you turn and look around in an HMD, you can easily move a few hundred degrees per second. You could detect these kind of rotations easily if you were standing still, but while walking or turning there's enough optic flow, head bob, and jarring from foot impact that the adjustments get lost in all the movment. Our non-visual spatial senses (e.g., inertial sensing by the inner ear, kinesthetic senses from your legs, etc.) have just enough noise in them that the visuals still appear to match.

Are all the cues visual or are the auditory or other cues that can be used?

Right now the cues we use are primarily visual, and to a lesser extent auditory, but it's easy to add in other senses if you have the ability. Since 3D audio emanates from a particular location in the virtual world, not the physical world, rotating the visuals brings all of the audio sources along with it. An active haptics display could work the same way, or a scent generator. Redirected walking essentially diverts the virtual camera, so any multisensory display that makes calculations based on your position in the virtual world will still work as expected. Adding more sensory feedback just reinforces what your eyes are seeing and should strengthen the effect.

What are practical applications of redirected walking? Is there a case study of someone using redirected walking outside an academic environment?

A gymnasium is about the smallest space you can work with and still curve people around without them noticing, so this is never going to run in your living room. We do have a portable, wearable version of our system with accurate foot-based position tracking that can be taken out of lab and used in, say, a park or a soccer field. It's a bit tricky, though, since the user is essentially running around the great outdoors blindfolded. If you're a liability lawyer for a VR goggle manufacturer, that's the kind of use case that gives you nightmares, but redirected walking could actually work in the gaming market with the right safety protocols. For example, we have safety mechanisms built in to our own systems, which usually includes a sighted escort and an automated warning system when users approach a pre-defined boundary. This could work in a controlled theme park or arcade-type setting, or with home-users that use some common sense. I can also see this technique being useful in industry and military applications. For example, the portable backpack system could easily be used for mission rehearsal in some remote corner of the globe. A squad of soldiers could each wear their own simulation rig and have their own ad-hoc tracking area to move around in. Likewise, some industry simulations incorporate large spaces and can benefit from physical movement. One scenario that came up a few years ago related to training repair technicians for large oil refineries, which can cover a square mile or more. Standing in a CAVE and pushing the forward button on a joystick just doesn't give you the same experience of having to actually walk a thousand meters across the facility while carrying heavy equipment, and then making a mission-critical repair under time pressure. Redirected walking would increase the realism of the training simulation without requiring a mile-square tracking area. Finally, I can see this benefiting the K-12 education system. Doing a virtual field trip in the gym would be pretty cool, and a responsible teacher or two could be present to watch out for the kids' safety.

Can redirected walking be applicable to augmented reality scenarios or just to immersive virtual reality?

It really doesn't make sense with augmented reality, in which you want the real and virtual worlds to be as closely aligned as possible. With redirected walking, the relationship between the real and virtual diverges pretty quickly. If you're doing large-scale navigation in AR, such as overlaying underground geological formations through a drill site, you'll want to actually navigate across the corresponding real-world space. It could make sense in some AR game situations, but it would be hard to make any continual, subtle adjustments to the virtual graphics without making them move perceptably relative to the real-world surroundings.

Is this technique applicable also to multi-person scenarios?

Definitely, and that's something we're actively exploring now. As long as you're redirecting people, and effectively steering where they go in the real world, there's no reason not to take several immersed people in the same tracking space and weave them in and around each other. Or, as I mentioned above with our portable system, if you can reliably contain people to a certain physical space with redirection, you can spread people out across a field and let everyone have their own little region while traveling through extremely large VEs. Adding multiple users does add some unexpected complexities, however. Under normal conditions, for example, when two immersed users come face to face in the VE, they would also be face to face in the physical world, and they could talk to each other normally, or reach out and touch each other, or share tools, etc. With redirected walking, those same users could be tens or hundreds of meters apart in the real world, requiring some sort of VOIP solution. By the same token, someone who is a mile away virtually might actually be very close to you, and you could hear them talking but not be able to see them, leading to an Uncanny Valley scenario.

How large or how small can a physical space be to implement successful redirected walking? Can this be used in a typical living room?

The HIVE is about 25m across in its narrowest dimension, which is about as small as you'd want to go. This is definitely not living-room material, which is where devices like the Omni will thrive instead. A lot of the literature recommends a space with a minimum radius of 30m+, which I think is about right. We have to stop people occasionally who are on a collision course with one of the lab's walls. A slightly larger space would let us catch and correct those trajectories automatically instead of manually stopping and redirecting the user. One thing to note is that the required tracking space interacts a lot with how much you turn up the redirection -- higher levels of steering constrain people to a smaller space, but they also become more noticeable. The type of VE and the user's task can also play a role. It seems like close-in environments like our virtual store make redirection more perceptible than open, visually ambiguous VEs like a virtual forest.

How immersive does an experience need to be for redirected walking to be successful?

High levels of immersion definitely help, but I'm not sure there's a certain threshold for success or failure here. Redirection relies on getting people to focus on their location in the virtual world while ignoring where they are in the room, and to innately accept their virtual movement as being accurate, even though it's not. Anytime you're in a decent HMD with 6-DOF tracking, the immersion level is going to be fairly high anyways, so this turns out to be a fairly easy task. As long as redirection is kept at reasonably low levels, it has been shown to work without being noticed, without increasing simulator sickness, and without warping people's spatial perception or mental map of the space.

Can you elaborate a bit on plans for future research in this area?

Right now the focus in our lab is on implementing mutli-user redirection and on improving the steering algorithms we use. We're also looking at behavioral prediction and virtual environment structure to try and predict where people might go next, or where they can't go next. For example, if I know you're in a hallway and can't turn for the next 10m, I can let you walk parallel to a physical wall without fear that you'll turn suddenly and hit it. There's a lot of other research going on right now in other labs that explore the perceptual limits of the effect and alternative methods of redirecting people. For example, it's possible to use an effect called "change blindness" to essentially restructure any part of the environment that's out of a person's view. So, if I'm looking at something on a virtual desk, the door behind me might move from one wall to another, causing me to leave alter my course by 90 degrees when I move to a different area. There's also a lot of work that's been done on catching potential wall collisions and gracefully resetting the user without breaking immersion too much.

For those that want to learn more about redirected walking, what other material would you recommend?

I'd really recommend reading Sharif Razzaque's early work on the topic, much of which he published with Mary Whitton out of UNC Chapel HIll. (http://scholar.google.com/scholar?q=razzaque+redirected+walking&btnG=&hl=en&as_sdt=0%2C36)

I'd also recommend reading some of Frank Steinicke's recent work on the techniques and perceptable limits of redirection (http://img.uni-wuerzburg.de/personen/prof_dr_frank_steinicke/), or some of our lab's work comparing higher-level redirection strategies such as steering people towards a central point versus steering people onto an ideal orbit around the room (http://www.users.miamioh.edu/hodgsoep/publications.php).

Finally, there's a good book that just came out on Human Walking in Virtual Environments that contains several good chapters on redirection as well as a broader look at the challenges of navigating in VEs and the perceptual factors involved. (http://www.amazon.com/Human-Walking-Virtual-Environments-Applications/dp/1441984313).

Eric, thank you very much for speaking with me. I look forward to learning more about your research in the future.

Redirected walking can save you from running into your sofa

A man is lost in the forest. No compass. No map. No phone. No GPS. He decides to walk in a straight line until he reaches a road. He walks and walks and walks until he can walk no more. When his body is found and the path he took is analyzed, it turns out that he was not actually walking in a straight, but going round and round in a big circle. Subtle visual cues - whether the forest, the earth or something else - fooled him into walking in a circle even though he intended to walk in a straight line.

There is no happy end here, but this man did not die in vein. It turns out that this same concept - of subtle visual cues - can direct a person in a virtual environment to take a certain path instead of  path that could lead to a collision.This is referred to as redirected walking.

Imagine a gamer wearing a virtual reality goggle. The true promise of goggles is in their portability and freedom of motion. Yes, most goggle users today sit deskside near a computer, but many experiences would be so much better if the user could roam around in a room, walk over, lean, pick up objects and so forth. But if a room has physical constraints to it such as a wall or a sofa, the person immersed in the goggle can collide in a way that would completely disrupt the experience, not to mention his leg or the sofa.

I had the opportunity to speak this week with Eric Hodgson, director at the Smale Interactive Visualization Center at Miami University of Ohio. Dr Hodgson is one of the leading researchers working on various aspects of redirected walking.

We got to this topic when discussing occlusion (see my previous blog post). One advantage of goggles that are not fully occluded is that the wearer feels safer when walking around because they can see the floor, some obstacles as well as other people around them. The downside of partial occlusion is that it reduces the sense of immersion. Dr. Hodgson's work shows, amongst other things, that immersion does not have to be traded off with safety. He has subjects walking around in a gym or even outside on a football field, being significantly immersed in an HMD. The visual stimuli presented in the HMD causes them to walk in a physical path that is different than what they perceive it to be.

Here is an image of a subject wearing an HMD with a computer on his back, fearlessly walking outside:

Courtesy of Dr. Eric Hodson, Miami University of Ohio

The following graph is even more interesting:

Redirected walking - Courtesy of Dr. Eric Hodson, Miami University of Ohio

The red line shows the actual physical path that a subject took. The blue line (dash-dot-dash) shows the visual path, the path that the subject thought he was taking inside the virtual world. As you can see, the subject ends up being confined in a space that is relatively small compared with the actual virtual space. 

Dr. Hodgson's research covers many aspects of this: what kind of cues are imperceptible to the person yet cause her to change her path; how is spatial memory impacted by this process of redirected walking and more.

Why is this useful? This concept is applicable to interactive games in several ways:

• It allows experiencing a large virtual world in spite of being constricted to a smaller physical space.
• It helps avoid physical obstacles (e.g. the sofa)
• It allows multiple people to be immersed in the same physical space without bumping into each other.

To read more about Dr. Hodgson's work, go to his publications page, and especially check out the 2013 Hodgson and Bachmann article.

Learn to master redirected walking, or find yourself stuck in the sofa.